Tanım
 boştan farklı bir evrensel küme olarak seçilsin. Bir
boştan farklı bir evrensel küme olarak seçilsin. Bir ![A:X \to [0,1]](http://upload.wikimedia.org/math/e/c/f/ecf1933a46755292cc0a740de6639222.png) fonksiyonuna
fonksiyonuna  üzerinde bir belirtisiz küme adı verilir.
üzerinde bir belirtisiz küme adı verilir.Belirtisiz küme farklı şekillerde de tanımlanabilir ancak kümenin her nokta için
![[0,1]](http://upload.wikimedia.org/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) kapalı aralığında bulunan bir üyelik değerine sahip olmasını anlatması bakımından bu tanımların hepsi birbirine denktir.
kapalı aralığında bulunan bir üyelik değerine sahip olmasını anlatması bakımından bu tanımların hepsi birbirine denktir.Bir
 ∈
∈ elemanı için
elemanı için 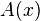 değerine
değerine  'in A'daki elemanlık derecesi denir. Bu değer kimi zaman
'in A'daki elemanlık derecesi denir. Bu değer kimi zaman  ile de gösterilir.
ile de gösterilir.  olması klasik küme anlamında
olması klasik küme anlamında  'in
'in  'nın elemanı olması,
'nın elemanı olması,  olması ise klasik kümelerdeki
olması ise klasik kümelerdeki  'in
'in  'nın elemanı olmaması durumuna denk gelir.
'nın elemanı olmaması durumuna denk gelir.Eğer bir
 için
için  ise
ise  ∈α
∈α yazılır ve
yazılır ve  'in
'in  belirtisiz kümesinin
belirtisiz kümesinin  derecesinde elemanı olduğu söylenir.
derecesinde elemanı olduğu söylenir.Örneğin
 yani
yani  ∈0,5
∈0,5 olması
olması  'in
'in  'nın yarı yarıya elemanı olması şeklinde yorumlanır. ∈1 klasik ∈, ∈0 klasik ∉ sembolüne karşılık gelir.
'nın yarı yarıya elemanı olması şeklinde yorumlanır. ∈1 klasik ∈, ∈0 klasik ∉ sembolüne karşılık gelir.Belirtisiz alt küme
 ve
ve  boş olmayan bir
boş olmayan bir  kümesi üzerinde iki belirtisiz küme olsun. Her
kümesi üzerinde iki belirtisiz küme olsun. Her  için
için  oluyorsa
oluyorsa  veya
veya  yazılır ve
yazılır ve  'nın
'nın  'nin bir belirtisiz alt kümesi olduğu söylenir.
'nin bir belirtisiz alt kümesi olduğu söylenir. ve
ve  belirtisiz kümelerinin eşitliği, her
belirtisiz kümelerinin eşitliği, her  ∈
∈  için
için  olmasıyla tanımlanır. Buna göre
olmasıyla tanımlanır. Buna göre  'nın
'nın  'ye eşit olması aynı zamanda hem
'ye eşit olması aynı zamanda hem  hem de
hem de 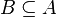 olması demektir.
olması demektir. üzerindeki bütün belirtisiz kümeler her
üzerindeki bütün belirtisiz kümeler her  ∈
∈ için
için  ile tanımlanan
ile tanımlanan  belirtisiz kümesinin alt kümesiyken, her
belirtisiz kümesinin alt kümesiyken, her  ∈
∈ için
için  ile tanımlanan
ile tanımlanan  belirtisiz kümesi
belirtisiz kümesi  'teki bütün belirtisiz kümelerin alt kümesidir. Bazen
'teki bütün belirtisiz kümelerin alt kümesidir. Bazen  ve
ve  sembolleri yerine sırasıyla
sembolleri yerine sırasıyla  ve
ve  veya kısaca
veya kısaca  ve
ve  kullanılır.
kullanılır.Belirtisiz kümeler üzerinde işlemler
Kümeler için tanımlı olan birleşim, kesişim, tümleme, kartezyen çarpım gibi işlemlerin tümü belirtisiz kümeler üzerine de taşınabilir.İki belirtisiz kümenin birleşimi
 veya
veya  ile gösterilir ve bu kümeye eleman olma derecesi her
ile gösterilir ve bu kümeye eleman olma derecesi her  ∈
∈ için
için  olarak tanımlanır.
olarak tanımlanır.İki belirtisiz kümenin kesişimi ise
 veya
veya 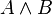 ile gösterilir ve bu kümeye eleman olma derecesi her
ile gösterilir ve bu kümeye eleman olma derecesi her  ∈
∈ için
için  olarak tanımlanır.
olarak tanımlanır. ve
ve  sırasıyla
sırasıyla  ve
ve  kümeleri üzerinde belirtisiz kümeler ise
kümeleri üzerinde belirtisiz kümeler ise 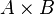 de
de  üzerinde bir belirtisiz kümedir ve her
üzerinde bir belirtisiz kümedir ve her  için
için  şeklinde tanımlanır.
şeklinde tanımlanır.İki küme için tanımlanan bu işlemler maksimum ve minimum yerine sırasıyla supremum ve infimum alınarak herhangi sayıdaki belirtisiz kümeler ailesine genişletilebilir.
 belirtisiz kümesinin tümleyeni
belirtisiz kümesinin tümleyeni 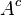 veya
veya 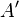 ile gösterilir ve her
ile gösterilir ve her  ∈
∈ için
için  formülüyle belirlenir. Klasik kümelerden farklı olarak bir
formülüyle belirlenir. Klasik kümelerden farklı olarak bir  belirtisiz kümesi için
belirtisiz kümesi için  olması mümkündür.(Vikipedi)
olması mümkündür.(Vikipedi)
Hiç yorum yok:
Yorum Gönder